一个数字签名体制都要包括_一个数字签名体制都要包括什么

一个数字签名体制都要包括_一个数字签名体制都要包括什么

       在接下来的时间里，我将尽力回答大家关于一个数字签名体制都要包括的问题，希望我的解答能够给大家带来一些思考。关于一个数字签名体制都要包括的话题，我们开始讲解吧。

1.电子签名中的数字签名是什么？

2.数字签名的基本流程是什么？

3.数字证书实一个经证书授权中心数字签名的包含()的文件

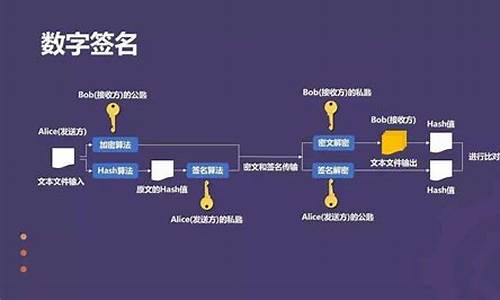
电子签名中的数字签名是什么？

       简单说，就是附加在数据单元上的一些数据,或是对数据单元所作的密码变换。做出这些改变后，数据接收者就可以确认数据完整性。

       这样的技术实现，就是数字签名。

       为了保证电子文件上的签名能够确认为当事人的真实意愿，防止盗用或篡改，需要一定的技术手段，通常是使用了公钥加密领域的技术实现。

数字签名的基本流程是什么？

       0、引言

       随着信息时代的到来,人们希望能通过网络信息传输对文

       件、契约、合同、信件和账单等进行数字签名来代替以往的手写

       签名。数字签名的目的是提供一种手段,使得一个实体把他的身

       份与某个信息捆绑在一起。一个消息的数字签名实际上是一个

       数,它仅仅依赖于签名者知道的某个秘密,也依赖于被签名信息

       本身。所以,将数字签名看成是一种证明签名者身份和所签署内

       容真实性的一段信息。

       1、RSA算法描述

       RSA算法是Rivest,Shamir和Adleman于1977年提出的比

       较完善的公钥密码系统。RSA算法是一个既能用于加密又能用

       于数字签名的公开密钥算法。RSA算法是基于这样一个数论事

       实:将两个大素数相乘十分容易,但是想分解它们的乘积却是困

       难的。

       RSA公钥加密的整个算法可以通过以下步骤来描述。

       1)生成两个大的素数p和q,p≠q;

       2)计算n=p×q,!(n)(p-1)(q-1);

       3)随机选择一个整数(公开的加密密钥),0<e<!(n),使得

       gcd(e,!(n))=1;

       4)计算满足下列条件(保密的解密密钥),ed=1mod!(n);

       5)对明文的加密运算是:c=E(m)=memodn;

       6)对密文的解密运算是:m=D(c)=cdmodn。

       此时公开(e,n)作为加密密钥E,自己保密(d,n)作为解密密钥

       D。隐藏p和q。

       2、RSA的保密性

       假设用户A获得了一对密钥变换(EA、DA),其中EA是可以

       公布于众的加密密钥,DA是由用户A自行秘密保管的解密密

       钥。当用户B要向用户A发送消息M时,B只需要找到EA,用它

       对消息M进行加密,C=EA(M),然后把密文C在公共信道上传

       送给A。当A收到密文C后,就用A秘密保管的解密密钥DA解

       密,DA(C)=DA(EA(M))=M,恢复出明文M。利用上述加密解密

       过程可使用户A和B之间达到保密传输。因为即使有窃听者获

       得了密文C,但是他没有解密密钥DA,所以不能恢复出明文M

       例如:

       如果用户A取p=7,q=71则n=pq=3337,!(n)(p-1)(q-1)=46×

       70=3220随机选取加密密钥e=79,则d=79-1。公开e和n,将d保

       密,隐藏p和q。设用户B要发给A的信息为m=688,用户B对m

       进行如下加密:c=68879mod3337=1570然后将密文c发给用户A

       用户A则利用保密的解密密钥进行如下解密:15701019mod3337=

       688=m。

       虽然这解决了用户A和B之间的保密传输,但是并没有解

       决可靠性,当A收到密文C时,并不能确定密文C就是用户B

       发来得。因为主动攻击的扰乱者也是知道用户A的加密密钥的

       因此扰乱者可以冒充B发一条假消息给A,这时A是无法判断

       该消息是否B发来的。这个问题可以利用数字签名来解决。

       3、RSA数字签名方案

       3.1公钥加密体制的数字签名原理

       其原理是:用户B用你的私钥来"加密"一组信息,用户A用公钥来解密,如果"解密"成功,说明这组信息就是用户B加密

       的,用户B无法否认这个事实,这就是数字签名。

       假设用户B获得了一对密钥变换(EB、DB),其中EB是可以公

       布于众的加密密钥,DB是由用户B自行秘密保管的解密密钥。

       当用户B要向用户A发送消息M时,如果用户B首先用自己保

       管的解密密钥DB作变换,C'=DB(M),然后把C'传送给A,当A

       收到密文C'后,可以用B的公开密钥EB作逆变换,EB(C')=EB

       (DB(M))=M,恢复出原始信息M。这样A就可以判断该消息一

       定是B发来的,因为只有B才知道秘密密钥DB,除B外,任何

       人都不能仿造信息C',因此C'可以作为用户B的数字签名,A可

       以通过EB来验证B的合法性,B对消息C'的确定性也是无法否

       认的。这样的应用只解决了消息的可靠性,可以防止第三者插

       入、伪造和篡改消息,但是并不能解决消息M的保密性,因为除

       了A以外,其他人也能收到,并恢复消息M。

       3.2保密性和可靠性的解决方案

       为了同时解决信息的保密性和可靠性这两个问题,我们可

       以对消息作如下处理:

       用户A和B分别获得了各自的密钥对(EA、DA)和(EB、DB),

       如果B要向A发送一条消息M,则可以先把消息M用B的秘

       密密钥DB处理,再用A的公开密钥EA加密,即C=EA(DB(M)),

       然后把C发送给A,A收到信息C后,先用自己的秘密密钥DA

       解C,再用B的公开密钥EB恢复,即

       EB(DA(C))=EB(DA(EA(DB(M))))=EB(DB(M))=M。

       把这两种方法如此地结合起来,用于加密信息,这样就可以

       到达人们预期的目的。使公共信道上传输的信息,即具有保密

       性,有具有可靠性,即可以防止第三者的被动窃取,又可以防止

       第三者的主动破坏,同时还具有认可和公证的能力。

       4、RSA安全性分析

       RSA的安全性依赖于大数分解的难度,目前因子分解速度

       最快的算法,其时间复杂性为exp(sqrt(n)1n1n(n))。若和为100位

       的十进制数,这样为200位十进制数,按每秒107次运算的超高

       速计算机,也要108年才能破解。因此,在一定有效期内,RSA数字

       签名是安全可靠的。2002年成功分解了158位的十进制数,故

       选取的素数p和q应该是长度为100的十进制数(相当于332

       位二进制数)。为了达到长期安全应该至少使用1024位。

       RSA的安全性受到的最大威胁就是整数素因子分解技术的

       发展,如果因素分解技术有了突破性发展,那么RSA的破解将会

       变得非常简单,可以直接计算出私钥。

       5、结束语

       数字签名有很多实现方法,目前广泛应用的主要有Hash签

       名,DSS签名,RSA签名,ElGamal签名。其中RSA签名是最流行

       的一种数字签名算法,尽管数字签名技术还不够完善,如签名后

       的文件可能被接收者重复使用,公开密钥加密算法的效率相当

       低,不易用于长文件的加密等。我们可以把RSA算法与其他算

       法(如DES算法)结合起来使用,既提高了他它的运行速度,又保

       证了一定的安全性。随着Internet的快速发展及其算法的不断改

       进和完善,其应用领域会日益广泛,有着广阔的发展前景。

数字证书实一个经证书授权中心数字签名的包含()的文件

       包括签名过程和验证签名过程。

       签名的实现过程：

       输入：原文、私钥

       输出：签名值

       1、将原文做HASH

       2、将HASH用私钥加密，结果就是签名值

       验证签名的实现过程：

       输入：签名值、原文、公钥

       输出：是否验证通过

       1、将原文做HASH1

       2、将签名值用公钥解密，取得HASH2

       3、将第1步的HASH1与第2步的HASH2做比较，两个HASH一样就验证通过，否则不通过

       数字证书是一个经证书授权中心数字签名的包含公钥拥有者信息已经公钥的文件。

       由于Inter网电子商务系统技术使在网上购物的顾客能够极其方便轻松地获得商家和企业的信息,但同时也增加了对某些敏感或有价值的数据被滥用的风险。

       为了保证互联网上电子交易及支付的安全性,保密性等，防范交易及支付过程中的欺诈行为，必须在网上建立一种信任机制。这就要求参加电子商务的买方和卖方都必须拥有合法的身份，并且在网上能够有效无误的被进行验证。

       数字证书是一种权威性的电子文档。它提供了一种在Inter上验证您身份的方式，其作用类似于司机的驾驶执照或日常生活中的身份证。

       它是由一个由权威机构----CA证书授权(Certificate Authority)中心发行的，人们可以在互联网交往中用它来识别对方的身份。当然在数字证书认证的过程中，证书认证中心（CA）作为权威的、公正的、可信赖的第三方，其作用是至关重要的。

       数字证书也必须具有唯一性和可靠性。为了达到这一目的，需要采用很多技术来实现。通常，数字证书采用公钥体制，即利用一对互相匹配的密钥进行加密、解密。

       今天关于“一个数字签名体制都要包括”的讨论就到这里了。希望通过今天的讲解，您能对这个主题有更深入的理解。如果您有任何问题或需要进一步的信息，请随时告诉我。我将竭诚为您服务。